
这道物理题目我才用解微分方程绘图的办法求解,可是两种方法原理都很正确参数也一致,绘制出的图像差别却很大
第一种(我做的)
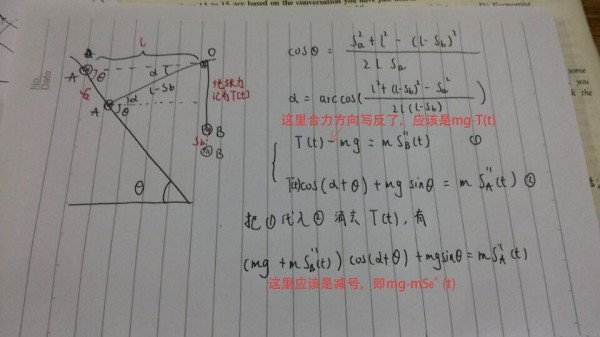
m = 1; L = 0.5; g = 10; \[Theta] = Pi/3;
Sb[t] = L - Sqrt[L^2 - 2 L Sa[t] Cos[\[Theta]] + Sa[t]^2];
\[Alpha] = ArcCos[(L^2 + (L - Sb[t])^2 - Sa[t]^2)/(2 L (L - Sb[t]))];
s = NDSolve[{g m Sin[\[Theta]] +
Cos[\[Alpha] + \[Theta]] (m g - m D[Sb[t], {t, 2}]) ==
m D[Sa[t], {t, 2}], Sa[0] == 0, (D[Sa[t], t] /. t -> 0) == 0},
Sa, {t, 0, 20}, PrecisionGoal -> 10];
Plot[Evaluate[Sa[t] /. s], {t, 0, 20}, PlotRange -> All]
Plot[Evaluate[D[Sa[t], t] /. s], {t, 0, 20}, PlotRange -> All]
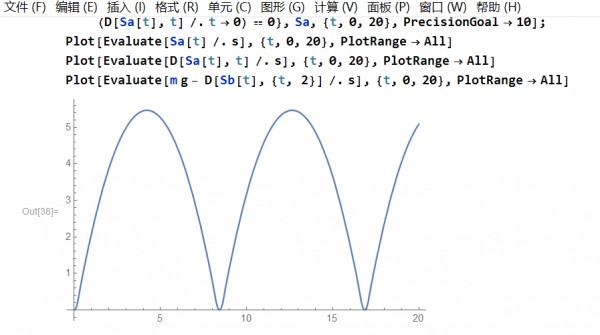
第二种(凡星有梦做法)
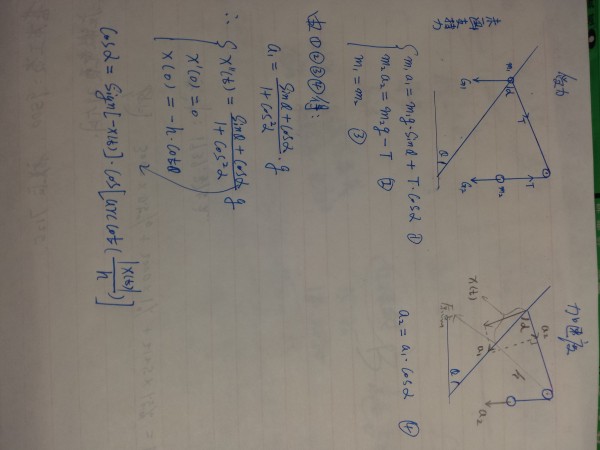
Quiet[Remove["Global`*"]];
Solve[{m1 a1 == m1 g Sin[\[Theta]] + T Sign[-x[t]] Cos[\[Alpha]],
m2 a2 == m2 g - T, a2 == Sign[-x[t]] a1 Cos[\[Alpha]]}, {a1, a2, T}]
(*得先告诉Mma哪些是变量,先求出a1的表达关系式*)
(为了便于理解,我把第四个关系式加上了Sign[-x[t]]来限定方向)然后把关系带入a1,运行下面的代码
Quiet[Remove["Global`*"]];
\[Theta] = Pi/3;
g = 10;
m1 = m2 = 1;
h = Sqrt[3]/
4;(*这里的\[Theta]=Pi/3,h=Sqrt[3]/4对应我的\[Theta]=Pi/3,L=0.\
5的情形,且坐标原点在h正下方,而我的坐标原点在m1初始位置处*)
t0 = 0;
t1 = 20;
\[Alpha] = ArcCot[Abs[x[t]]/h];
a1 = -((g m2 Cos[\[Alpha]] Sign[x[t]] - g m1 Sin[\[Theta]])/(
m1 + m2 Cos[\[Alpha]]^2 Sign[x[t]]^2));
s = NDSolve[{x''[t] == a1, x'[0] == 0, x[0] == -h Cot[\[Theta]]},
x, {t, t0, t1}];
Plot[{Evaluate[x[t] /. s], Evaluate[x'[t] /. s]}, {t, t0, t1},
PlotLegends -> {"位移(向下为正)", "速度"}]
但是他的位移幅值和周期和我的明显不同,我查了半天,并没有找到推导错误,想知道是不是NDSolve求解的误差或者是我的代码哪里写错了
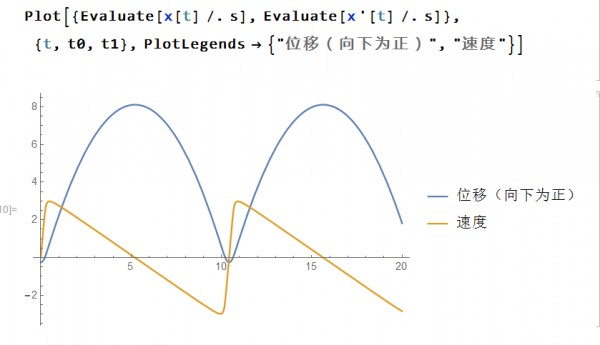
请社区朋友帮忙看一下,指出我的错误
经过一上午的努力,发现问题所在了,凡星有梦的加速度分解是错误的,貌似少了牵连加速度或者相对加速度
理论力学有一章讲这个的,另外我在知网找到的相关论文截图如下,谢谢大家
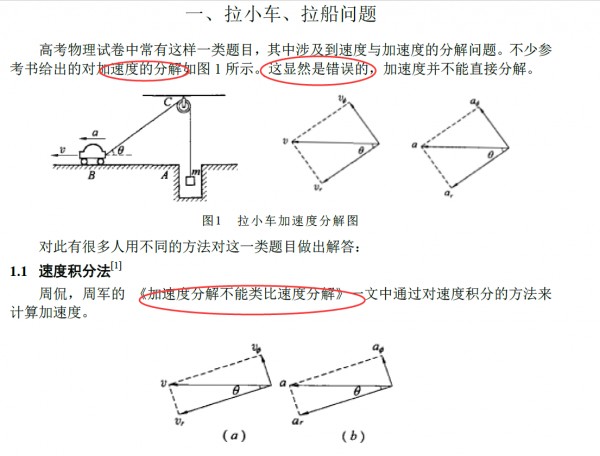

明显少了一项,稍后我把凡星有梦的代码修改一下,大家也可以根据正确的加速度关系,修改一下,最后对比一下,万分感谢大家
今天上午我对加速度关系进行了修正,可是依然无法绘图
Quiet[Remove["Global`*"]];
Solve[{m1 a1 == m1 g Sin[\[Theta]] + T Sign[-x[t]] Cos[\[Alpha]],
m2 a2 == m2 g - T,
a2 + (x'[t]^2 Sin[\[Alpha]]^2)/(x[t]^2 + h^2)^(1/2) ==
a1 Cos[\[Alpha]]}, {a1, a2, T}]
得出a1表达式后,运行下列代码
Quiet[Remove["Global`*"]];
\[Theta] = Pi/3;
g = 10;
m1 = m2 = 1;
h = Sqrt[3]/
4;(*这里的\[Theta]=Pi/3,h=Sqrt[3]/4对应我的\[Theta]=Pi/3,L=0.\
5的情形,且坐标原点在h正下方,而我的坐标原点在m1初始位置处*)
t0 = 0;
t1 = 10;
\[Alpha] = ArcCot[Abs[x[t]]/h];;
(*v^2=(Sign[-x[t]]x'[t]Cos[\[Alpha]])^2;*)
(*V=Sign[-x[t]]x'[t]Cos[\[Alpha]]*)
a1 = -((g m2 Cos[\[Alpha]] Sign[x[t]] - g m1 Sin[\[Theta]] - (
m2 Cos[\[Alpha]] Sign[x[t]] Sin[\[Alpha]]^2 Derivative[1][x][t]^2)/
Sqrt[h^2 + x[t]^2])/(m1 - m2 Cos[\[Alpha]]^2 Sign[x[t]]))
s = NDSolve[{x''[t] == a1, x'[0] == 0, x[0] == -h Cot[\[Theta]]},
x, {t, 0, t1}];
Plot[{Evaluate[x[t] /. s], Evaluate[x'[t] /. s],
Evaluate[m1 x'[t]^2/2 + (-m1 g x[t] Sin[\[Theta]]) /. s]}, {t, t0,
t1}, PlotLegends -> {"位移(向下为正)", "速度", "机械能"}]
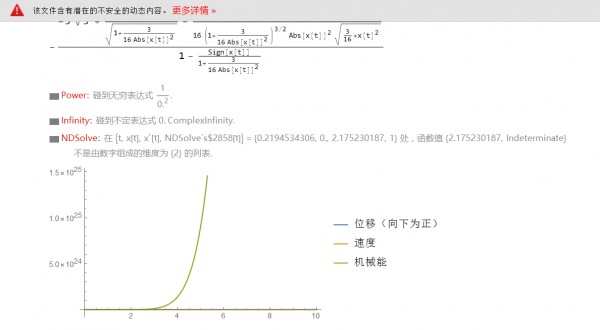
看了很久我没有发现理论错误,请大家帮忙再看一下...
加速度项已经更正
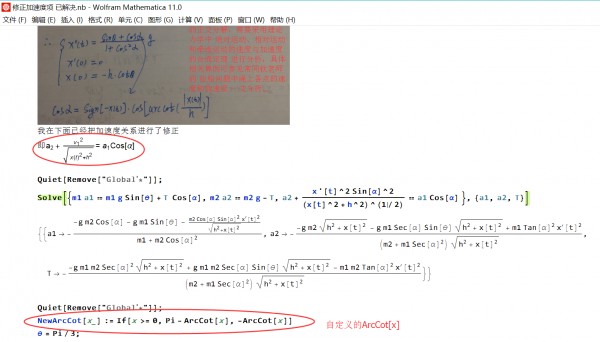
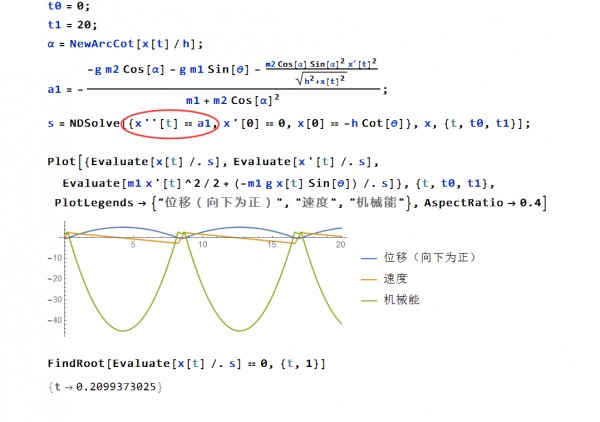
Quiet[Remove["Global`*"]];
NewArcCot[x_] := If[x >= 0, Pi - ArcCot[x], -ArcCot[x]]
\[Theta] = Pi/3;
g = 10;
m1 = 1;
m2 = 1;
h = Sqrt[3]/
4;(*这里的\[Theta]=Pi/3,h=Sqrt[3]/4对应我的\[Theta]=Pi/3,L=0.\
5的情形,且坐标原点在h正下方,而我的坐标原点在m1初始位置处*)
t0 = 0;
t1 = 20;
\[Alpha] = NewArcCot[x[t]/h];
Solve[{m1 a1 == m1 g Sin[\[Theta]] + T Cos[\[Alpha]],
m2 a2 == m2 g - T,
a2 + (x'[t]^2 Sin[\[Alpha]]^2)/(x[t]^2 + h^2)^(1/2) ==
a1 Cos[\[Alpha]] }, {a1, a2, T}][[1, 1]] /. Rule -> Set;
s = NDSolve[{x''[t] == a1, x'[0] == 0, x[0] == -h Cot[\[Theta]]},
x, {t, t0, t1}];
Plot[{Evaluate[x[t] /. s], Evaluate[x'[t] /. s],
Evaluate[m1 x'[t]^2/2 + (-m1 g x[t] Sin[\[Theta]]) /. s]}, {t, t0,
t1}, PlotLegends -> {"位移(向下为正)", "速度", "机械能"}, AspectRatio -> 0.4]

