如何通过级数展开或者编译之类的优化这个函数？

Question

这是一个定义在复数底，高为实数的超-4运算（或者说迭代幂次运算，幂塔函数）：

(*原作者Andrew Robbins*)

TetratePrepare[n_Integer, x_] := {x, LinearSolve[
   Table[k^j/k! - If[j == k, Log[x]^-k, 0], {j, 0, n - 1}, {k, 1, n}],
    Table[If[k == 1, 1, 0], {k, 1, n}]]}
(*产生高度为(-1,0]的实数的时候的特征信息，n为微分精度，x为底*)
    
SuperLog[v_, z_?NumericQ] := 
 Block[{(*SlogCrit*)}, 
  SlogCrit[zc_] := -1 + Sum[v[[2, k]]*zc^k/k!, {k, 1, Length[v[[2]]]}];
  Which[z <= 0, SlogCrit[v[[1]]^z] - 1, 0 < z <= 1, SlogCrit[z], 
   z > 1, Block[{i = -1}, 
    SlogCrit[NestWhile[Log[v[[1]], #] &, z, (i++; # > 1) &]] + i]]]
(*幂塔函数的反函数.使用方法为SuperLog[TetratePrepare[精度,底],高]*)

Tetrate[v_, y_?NumericQ] := 
 Block[{(*SlogCrit,TetCrit*)}, 
  SlogCrit[zc_] := -1 + Sum[v[[2, k]]*zc^k/k!, {k, 1, Length[v[[2]]]}];
  TetCrit[yc_] := FindRoot[SlogCrit[z] == yc, {z, 1}][[1, 2]]; 
  If[y > -1, 
   Nest[Power[v[[1]], #] &, TetCrit[y - Ceiling[y]], Ceiling[y]], 
   Nest[Log[v[[1]], #] &, TetCrit[y - Ceiling[y]], -Ceiling[y]]]]
(*幂塔函数.使用方法为Tetrate[TetratePrepare[精度,底],高]*)

可以看到这个定义是依照可微性定义的，n决定这个函数可以做多少次微分之后依然连续，当n无穷大的时候便是所需要的无穷可微，但是这个定义的阻碍也是在于此：当需要的输出精度提升一点时，TetratePrepare的n就需要比较大的上升，然而n的上升将严重影响到整个函数的性能。（6位有效数字左右的输出，n大于150才准确）

====================================================================================

精度对照表：

定义幂塔运算符为：（n->∞，h为高，a为底，书写的不标准什么的不要在意）

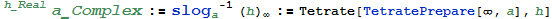
那么有精度表：

明显可见精度n的增加会随着h和a的增加而增加。

对于5位有效数字，本表的例子需要n在8,20,30,70不等；

6位需要n在30,50,90不等；

7位需要n在130左右；

8位140~150以上。

现在来测速，令h=a=E：

In[257]:= NumberForm[Tetrate[TetratePrepare[30,E],E],16]//AbsoluteTiming
NumberForm[Tetrate[TetratePrepare[50,E],E],16]//AbsoluteTiming
NumberForm[Tetrate[TetratePrepare[130,E],E],16]//AbsoluteTiming
NumberForm[Tetrate[TetratePrepare[140,E],E],16]//AbsoluteTiming
NumberForm[Tetrate[TetratePrepare[200,E],E],16]//AbsoluteTiming
NumberForm[Tetrate[TetratePrepare[233,E],E],16]//AbsoluteTiming
NumberForm[Tetrate[TetratePrepare[250,E],E],16]//AbsoluteTiming
NumberForm[Tetrate[TetratePrepare[314,E],E],16]//AbsoluteTiming
NumberForm[Tetrate[TetratePrepare[350,E],E],16]//AbsoluteTiming
NumberForm[Tetrate[TetratePrepare[400,E],E],16]//AbsoluteTiming
NumberForm[Tetrate[TetratePrepare[444,E],E],16]//AbsoluteTiming
Out[257]= {0.0144852,2075.998583292668}
Out[258]= {0.123252,2075.968983446195}
Out[259]= {2.04883,2075.968051571146}
Out[260]= {2.90037,2075.968108549399}
Out[261]= {22.7724,2075.968255391066}
Out[262]= {43.2987,2075.968287381941}
Out[263]= {54.9554,2075.968297523795}
Out[264]= {199.563,2075.968318425804}
Out[265]= {326.491,2075.968323984475}
Out[266]= {673.932,2075.968328436254}
Out[267]= {1281.27,2075.968330769448}

恩打脸打得好爽。。。n=140有个屁8位有效数字。差不多n=350才有8位有效数字，320+可以说慢到可以了

===================================================================

更新问题：

1.能不能用mma的命令求出Tetrate[TetratePrepare[n,a],h]（其中n为给定的一个充分大的数）的级数展开形式？（这可是个正二八经的二元函数）

2.能不能优化/编译/并行化Tetrate[TetratePrepare[n,a],h]这个函数？

 

Comments

那回到第一个问题，如何求它的级数展开？

---

实不相瞒第一个问题并没看明白，你是说要用级数展开来近似TetratePrepare？也就是用级数近似来解一个线性方程组？……有这种技术吗？

---

更新了下问题。近似TetratePrepare当然不可能，但是近似Tetrate[TetratePrepare[n,a],h]（其中n为给定的一个充分大的数）应该是。。可以的吧？这可是个正二八经的二元复函数

---

折叠内容不显示。折叠内容不显示。

---

@matmma 问题主的初始问题描述中有句“8位140~150以上”。在我要求提供测试对比数据以后，发现“n=140有个屁8位有效数字。差不多n=350才有8位有效数字”，因此问题主表示打了自己脸。

Answer 1

这里提供一个不稳定(需要人为确定一个参数)加速方法。

仔细观察，整个程序运行的时间，99%是TetratePrepare，所以其他部分程序一概不看。TetratePrepare这部分比较简单，Table + LinearSolve。所以99%的运行时间是LinearSolve，这个评论已经说了无法并行+编译。

但问题是，你原来使用的是无限精度的符号计算（所以结果是分数表达式，并且计算速度很慢）。但是基于你后续计算是浮点计算，所以此处可以考虑也使用浮点计算，但是显然机器精度是不够的，所以需要增加精度。做一下改变（m是N的精度，设置m=2n是随便写的，实际上到底应该设置为多少，我也不清楚，有待探讨）。

Clear["Global`*"];
TetratePrepare[n_Integer, x_] := {x, 
   LinearSolve[
    Table[k^j/k! - If[j == k, Log[x]^-k, 0], {j, 0, n - 1}, {k, 1, 
      n}], Table[If[k == 1, 1, 0], {k, 1, n}]]};

TetratePrepare2[n_Integer, x_] := 
 Block[{m = 2 n}, {x, 
   LinearSolve[
    N[Table[k^j/k! - If[j == k, Log[x]^-k, 0], {j, 0, n - 1}, {k, 1, 
       n}], m], Table[If[k == 1, 1, 0], {k, 1, n}]]}]
       
(*SuperLog和Tetrate函数未做改动*)

getData[n_] := 
  AbsoluteTiming[
      NumberForm[Tetrate[#[n, E], E], 16]] & /@ {TetratePrepare, 
     TetratePrepare2} // Flatten;
     
TableForm[getData /@ {30, 50, 130, 200}, 
 TableHeadings -> {{"n=30", "n=50", "n=130", "n=200"}, {"t1", 
    "TetratePrepare", "t2", "TetratePrepare2"}}]

当n=400时，m=2n已经不足够了，设置成m=3n，得到结果为

{71.5433,2075.968328436254}

Comments

非常有用。近似值应该取多少的问题，我可以以后慢慢测试解决。