Clear["Global`*"]
data = {{{-2.`, -5.6`*^-10}, {-1.8`, -4.`*^-10}, {-1.6`, \
-1.1000000000000001`*^-10}, {-1.4`, 1.05`*^-9}, {-1.2`,
3.59`*^-9}, {-1.`, 6.75`*^-9}, {-0.8`, 1.036`*^-8}, {-0.6`,
2.53`*^-8}, {-0.4`, 3.69`*^-8}, {-0.2`,
4.7000000000000004`*^-8}, {0.`, 5.83`*^-8}, {0.2`,
6.69`*^-8}, {0.4`, 7.180000000000001`*^-8}, {0.6`,
7.57`*^-8}, {0.8`, 7.920000000000001`*^-8}, {1.`,
8.2`*^-8}, {1.2`, 8.48`*^-8}, {1.4`, 8.63`*^-8}, {1.6`,
8.9`*^-8}, {1.8`, 9.100000000000001`*^-8}, {2.`,
9.34`*^-8}}, {{-2.`, -1.14`*^-9}, {-1.8`, -9.6`*^-10}, {-1.6`, \
-2.09`*^-9}, {-1.4`, 1.5000000000000002`*^-9}, {-1.2`,
4.8`*^-9}, {-1.`, 1.02`*^-8}, {-0.8`,
2.0300000000000003`*^-8}, {-0.6`, 3.13`*^-8}, {-0.4`,
4.9200000000000004`*^-8}, {-0.2`, 6.42`*^-8}, {0.`,
8.500000000000001`*^-8}, {0.2`, 1.0699999999999999`*^-7}, {0.4`,
1.3`*^-7}, {0.6`, 1.34`*^-7}, {0.8`, 1.8`*^-7}, {1.`,
1.9`*^-7}, {1.2`, 2.19`*^-7}, {1.4`, 2.48`*^-7}, {1.6`,
2.69`*^-7}, {1.8`, 2.92`*^-7}, {2.`, 3.18`*^-7}}, {{-2.`,
6.72`*^-11}, {-1.8`, 6.52`*^-11}, {-1.6`, 6.4`*^-11}, {-1.4`,
5.67`*^-11}, {-1.2`, 3.31`*^-11}, {-1.`,
3.9799999999999994`*^-11}, {-0.8`, 2.28`*^-10}, {-0.6`,
6.05`*^-10}, {-0.4`, 1.2`*^-9}, {-0.2`,
2.1100000000000004`*^-9}, {0.`, 3.25`*^-9}, {0.2`,
4.55`*^-9}, {0.4`, 5.970000000000001`*^-9}, {0.6`,
7.33`*^-9}, {0.8`, 8.83`*^-9}, {1.`, 1.15`*^-8}, {1.2`,
1.3600000000000001`*^-8}, {1.4`, 1.56`*^-8}, {1.6`,
1.7200000000000002`*^-8}, {1.8`, 1.9`*^-8}, {2.`,
2.09`*^-8}}, {{-2.`, -2.0899999999999997`*^-11}, {-1.8`, \
-2.0600000000000002`*^-11}, {-1.6`, -2.04`*^-11}, {-1.4`, \
-2.05`*^-11}, {-1.2`, -2.03`*^-11}, {-1.`, -1.94`*^-11}, {-0.8`, \
-1.8699999999999997`*^-11}, {-0.6`, 9.300000000000001`*^-12}, {-0.4`,
3.09`*^-11}, {-0.2`, 1.7399999999999997`*^-10}, {0.`,
5.62`*^-10}, {0.2`, 1.1699999999999999`*^-9}, {0.4`,
2.0600000000000003`*^-9}, {0.6`, 2.9`*^-9}, {0.8`,
3.91`*^-9}, {1.`, 4.86`*^-9}, {1.2`, 5.84`*^-9}, {1.4`,
6.56`*^-9}, {1.6`, 7.340000000000001`*^-9}, {1.8`,
7.91`*^-9}, {2.`,
8.33`*^-9}}, {{-2.`, -7.`*^-12}, {-1.8`, -6.9`*^-12}, {-1.6`, \
-7.`*^-12}, {-1.4`, -6.599999999999999`*^-12}, {-1.2`, -6.4`*^-12}, \
{-1.`, -6.2999999999999994`*^-12}, {-0.8`, \
-6.2999999999999994`*^-12}, {-0.6`, -4.8`*^-12}, {-0.4`,
1.3000000000000001`*^-12}, {-0.2`, 2.6`*^-11}, {0.`,
1.19`*^-10}, {0.2`, 3.0999999999999996`*^-10}, {0.4`,
5.5`*^-10}, {0.6`, 8.609999999999999`*^-10}, {0.8`,
1.0800000000000002`*^-9}, {1.`, 1.35`*^-9}, {1.2`,
1.6300000000000002`*^-9}, {1.4`, 1.85`*^-9}, {1.6`,
2.0600000000000003`*^-9}, {1.8`, 2.23`*^-9}, {2.`,
2.3399999999999998`*^-9}}};
c = 299792458;
v = c 10^9/{365, 405, 436, 546, 577};
e = 1.6 10^-19;
pc = {365, 405, 436, 546, 577};
jl2[x_List] := (x[[1]][[2]] - x[[2]][[2]])/(x[[1]][[1]] - x[[2]][[1]]);
ModDistance2[x_] := jl2[{#1, #2}] &[Sequence @@ x]
fg[x_List] :=
Module[{l = Length@x}, Table[{x[[i]], x[[i + 1]]}, {i, 1, l - 1}]]
t = FindClusters[ModDistance2 /@ (fg@data[[#]]), 3] & /@ Range[5];
add[x_List] := Table[Tr@(x[[;; i]]), {i, 1, Length@x}];
d[x_List] :=
Module[{l = Length@x, r}, r = Table[Length@x[[i]], {i, 1, l}];
Prepend[add[r], 1]]
sp[x_List, y_List] := {x[[;; y[[2]] + 1]],
x[[y[[2]] + 2 ;; y[[3]] + 1]], x[[y[[3]] + 2 ;;]]}
tj = ListPlot[#,
PlotMarkers -> {"\[FilledSquare]", "\[FilledCircle]",
"\[FilledUpTriangle]"}] & /@ (sp[data[[#]], d[t[[#]]]] & /@
Range[5])
不知道为什么这个程序每次运行都不一样 找了很久发现好像是FindClusters 出了问题 大家能解释一下吗？
这个程序的目的是想取将一组点中线性关系相近的点取出来
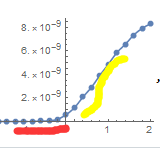比如图中的点，我想把红色斜率较低的点和黄色斜率较高的点分开
