这个问题其实挺有意思的。所以我修改了问题名。
Ellipsoid毫无疑问可以绘画倾斜的椭圆。但是帮助文档里几乎没有倾斜椭圆的例子(只有1个,还看不懂)。
再查帮助文档Ellipsoid,发现“更多信息”中对Ellipsoid的两种语法都做了解释:

第一种显然就是正的椭圆了。第二种是什么东西?所以先做个试验,为简单,p取为0,并给∑取一个对称矩阵。
{x, y}.Inverse[{{a, b}, {b, d}}].{x, y} <= 1 // Expand
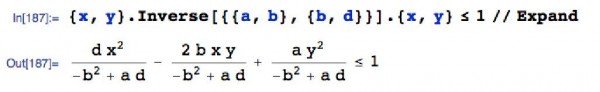
所以只要a,b,d的值取得好,那么我们就可以画出任意倾斜的椭圆。问题是,已知长短轴,怎么计算a,b,d。
倾斜椭圆可以看成是正椭圆的旋转,所以已知长短轴可以写出另外一个表达式。
x^2/c1^2 + y^2/c2^2 /. {x -> x Cos[θ] - y Sin[θ],
y -> y Cos[θ] + x Sin[θ]} // Expand // Collect[#, {x, y}] &
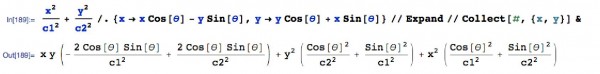
分别令x^2,y^2和xy之前的系数与前一个表达式的系数相等,就可以解出来合适的a,b,d了。
getCoeff[vec1_, vec2_] := Module[{c1, c2, θ},
c1 = Norm@N@vec1; c2 = Norm@N@vec2; θ = ArcTan @@ N[vec1];
Off[Solve::ratnz];
First@Solve[{d/(-b^2 + a d) ==
Cos[θ]^2/c1^2 + Sin[θ]^2/c2^2, (
2 b)/(-b^2 + a d) == -((2 Cos[θ] Sin[θ])/c1^2) + (2 Cos[θ] Sin[θ])/c2^2,
a/(-b^2 + a d) == Cos[θ]^2/c2^2 + Sin[θ]^2/c1^2}, {a, b, d}]
]
然后就可以画图了。
mat = {{a, b}, {b, d}} /. getCoeff[sigma1u1, sigma2u2];
Graphics[{Black, FaceForm[Opacity@.2], Ellipsoid[{0, 0}, mat],
Arrow[{{0, 0}, sigma1u1}], Arrow[{{0, 0}, sigma2u2}]}, Axes -> True]
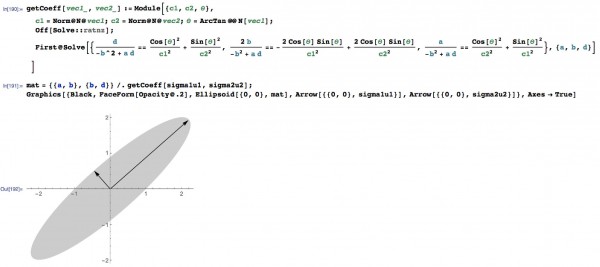
最后可以重载Ellipsod函数,使得我们可以直接输入长短轴的矢量进行画图,而不是我不懂的∑函数。
Clear["Global`*"]
(*重载Ellipsoid函数,增加一个画椭圆的语法,并修改自动配色*)
ClearAttributes[Ellipsoid, Protected];
Ellipsoid[r_, vec1_, vec2_] := Module[{c1, c2, mat, θ, a, b, d},
Ellipsoid::nnarg = "请输入正交的椭圆长短轴";
If[Chop[vec1.vec2] != 0, Message[Ellipsoid::nnarg]];
c1 = Norm@N@vec1; c2 = Norm@N@vec2; \[Theta] = ArcTan @@ N[vec1];
mat = {{a, b}, {b, d}} /.
First@NSolve[{d/(-b^2 + a d) == Cos[θ]^2/c1^2 + Sin[θ]^2/c2^2,
(2 b)/(-b^2 + a d) ==
-((2 Cos[θ] Sin[θ])/c1^2) + (2 Cos[θ] Sin[θ])/c2^2,
a/(-b^2 + a d) == Cos[θ]^2/c2^2 + Sin[θ]^2/c1^2}, {a, b, d}];
Ellipsoid[r, mat]
];
SyntaxInformation[Ellipsoid] = {"ArgumentsPattern" -> {__}};
SetAttributes[Ellipsoid, Protected];
(*生成相互垂直的两个矢量作为长短轴,以及椭圆中心点*)
{r1, r2} = RandomReal[{0, 10}, 2];
θ = RandomReal[{0, 2 Pi}];
vec1 = r1 {Cos[θ], Sin[θ]}; vec2 = r2 {Cos[θ + Pi/2], Sin[θ + Pi/2]};
p = RandomReal[{-10, 10}, 2];
(*画图*)
Graphics[{Black, FaceForm[Opacity@.2], Ellipsoid[p, vec1, vec2],
Arrow[{p, vec1 + p}], Arrow[{p, vec2 + p}]}, Axes -> True]

