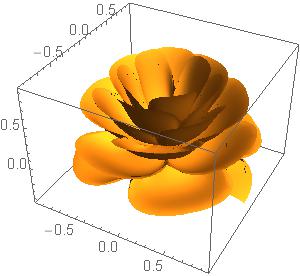
1. 今天深究了一下这个问题,发现源代码中ParametircPlot3D这句话如果完全不改得到的图,其实是个美丽的错误,也就是说这个图与函数并不相符。
首先是一些常规定义,将最终的函数表达式命名为expr。
p = Pi/2 Exp[-(t/(8 Pi))];
u = 1 - 1/2 (1 - Mod[3.6 t, 2 Pi]/Pi)^4;
y = 2 (x^2 - x)^2 Sin[p];
r = u (x Sin[p] + y Cos[p]);
expr = {r Cos[t], r Sin[t], u (x Cos[p] - y Sin[p])};
2. 其次可以发现expr就是一堆简单计算,可以使用compile加速。
cf = With[{expr = N@expr}, Compile[{{t, _Real}, {x, _Real}}, expr]];
3. 然后验证一下cf和expr之间的误差,处于机器精度级别,可以忽略。
Table[Evaluate@expr - cf[t, x], {t, -2 Pi, 15 Pi, 0.2}, {x, 0, 1,
0.005}] // Abs // Flatten // Total
(*1.9026*10^-11*)
4. 然后就可以画图了。下面用表列出了画图的时间、图的点数。
SetOptions[ParametricPlot3D, Mesh -> None];
p1 = AbsoluteTiming[ParametricPlot3D[expr, {t, -2 Pi, 15 Pi}, {x, 0, 1}]];
p2 = AbsoluteTiming[
ParametricPlot3D[cf[t, x], {t, -2 Pi, 15 Pi}, {x, 0, 1},
PlotPoints -> 45]];
Grid[{{"point number", "timing", "picture"}, {Length@p1[[2, 1, 1]],
First@p1, p1[[2]]}, {Length@p2[[2, 1, 1]], First@p2, p2[[2]]}},
Frame -> All, Alignment -> Center]
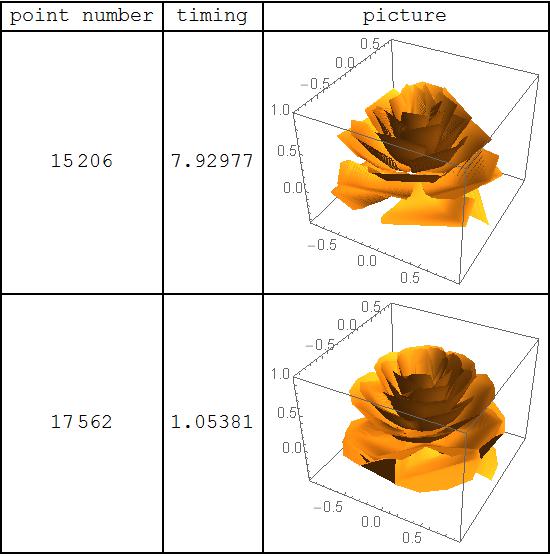
5. 可以发现,在点数相同的情况下,好像cf出来的图很丑,远没有expr的漂亮,expr的花瓣都是分开的,而且有点像多边形。实际上呢?来个细节图。
SetOptions[
ParametricPlot3D, {Mesh -> None, ViewPoint -> {0, 0, Infinity},
ImageSize -> 200}];
p1 = ParametricPlot3D[expr, {t, -2 Pi, 0}, {x, 0, 0.1}, PlotPoints -> 60];
p2 = ParametricPlot3D[cf[t, x], {t, -2 Pi, 0}, {x, 0, 1}, PlotPoints -> 55];
Grid[{{"p1 point:", "p2 point:"}, {Length@p1[[1, 1]],
Length@p2[[1, 1]]}, {p1, p2}}]
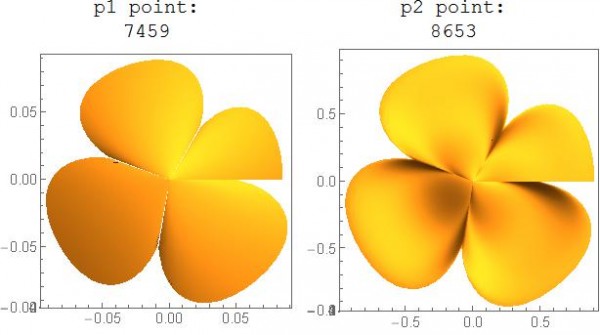
6. 可以看到,如果看细节图,就知道其实每个花瓣是圆弧形的,而且相互之间是完全连在一起的!所以最初的那个ParametircPlot3D得到的图,是完全错误的!
7. 那么完全正确的图是什么样的呢?是下面这样的(其实PlotPoint设置为200仍然不够,花瓣之间还是有些问题)。
SetOptions[
ParametricPlot3D, {Mesh -> None, ViewPoint -> {1.3, -2.4, 2}}];
ParametricPlot3D[cf[t, x], {t, -2 Pi, 11 Pi}, {x, 0, 1},
PlotPoints -> 200]