先发代码:
xyz = {0.292955, 0.27291, 0.434135};
data = {#, Total[(# - Round@#)^2]/3 &[# xyz]} & /@ Range[1, 1000, 0.1];
len = Length@data;
sigma = 1;
ans = If[Last@# < sigma,
Sow@{#, Round[xyz First@#],
k = xyz.Round[xyz First@#]/(#.# &@
xyz), #.# &@(# - Round@# & /@ (k xyz))/3};
sigma = Last@#] & /@ data // Reap // Last // Last //
DeleteDuplicates[#, Last@#1 == Last@#2 &] &;
TableForm[Flatten /@ ans,
TableHeadings -> {None, {"k-approx", "\[Sigma]-approx", "a", "b",
"c", "k", "\[Sigma]"}},
TableAlignments -> Center]
运行结果为
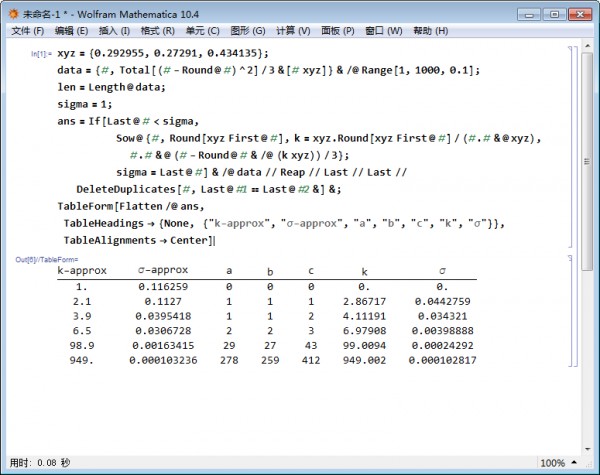
====================以下是我的思路的分割线(太长不看)====================
首先,原始的数据应为{a,b,c},然而由于实验误差,测得的值为{a+e,b+e,c+e}(e为服从NormalDistribution[0,sigma]的正态分布变量),再放缩至{a+e,b+e,c+e}/k(注意这里k可以是任意实数而不限于正整数),最后表现为{x,y,z}的形式。
那么,如何从{x,y,z}还原至{a,b,c}呢?先需要放大至k{x,y,z},用Round[k{x,y,z}]来拟合{a,b,c}的值,其偏离值#-Round@#&/@(k{x,y,z}可视为e的三次取样,不防设为d1,d2,d3。由概率统计中的极大似然思想,可知三次取样为d1,d2,d3服从的正态分布的参数sigma^2的估计值为(d1^2+d2^2+d3^2)/3。显然sigma越小,拟合效果越好。
这就有点思路了,可以让k逐渐增大,对每个k可以对应一个sigma的估计值。而我们的目的是要找最接近{x,y,z}比例的{a,b,c},也即任给{a1,b1,c1}<{a,b,c},对应的sigma1>sigma。换句话说,在sigma=f[k]这个函数中找到某个特定的k0,对应的sigma0是k取[1,k0]间的值的最小值,即k<k0时必有f[k]<f[k0]。此时对应的{a,b,c}即是比之前拟合效果更好的拟合。
然而,sigma=f[k]=#.#&@(#-Round@#&/@(k{x,y,z}))/3,这样涉及数论函数Round的一个式子无法用导函数为0的方法求出k值。果断耍个流氓,先对k值离散化,用k=Range[1,1000,0.1]来求出一系列的sigma值,然后找出所有sigma0使得sigma0比前面的sigma值都小,即为一个局部极小值的近似值,此时对应的{a,b,c}即为所求。以此k值(即图中的k-approx)为初值求出真正使得sigma0值最小的k和sigma即可。根据sigma=(kx-a)^2+(ky-b)^2+(kz-c)^2,k作微小改变时{a,b,c}不会改变(否则k{x,y,z}必有一个接近n+0.5,此时sigma值必然很大,矛盾),可将a,b,c视作常数并对k求导,于是k=(ax+by+cz)/(x^2+y^2+z^2)时即为k-approx附近的极小值点,并以此计算出sigma即可。
上述代码就是基于这个思路来写的。先找出所有sigma近似最小值及对应的k近似值,以此算出{a,b,c},去重(可能会有好几个k对应同一组{a,b,c}),最后算出真正的k和sigma。
做出表格后,可根据需要的sigma值为基准进行选择,比如只要sigma^2>0.004即可,那{2,2,3}即为满足需要的整数比;若要求sigma^2取0.001,则需要的整数比应为{29,27,43},以此类推。