V0
目测是没有解析解的,那就数值求解吧。
solve[{x0_, y0_}] /; (y0 != x0) :=
Quiet@Check[
FindRoot[{D[h2[t1, t2], t1] == 0,
D[h2[t1, t2], t2] == 0}, {{t1, x0}, {t2, y0}}], {}];
solve[{x0_, y0_}] /; (y0 == x0) := {};
sol = Partition[
Flatten@Table[solve[{x0, y0}], {x0, 0, 16, 0.2}, {y0, 0, 16, 0.2}],
2];
p = Select[{t1, t2} /. DeleteDuplicates[sol],
0.01 <= #1 <= 16 && 0.01 <= #2 <= 16 & @@ # &];
这是找到了所有的导数为0的地方,还需要进行一次筛选,才能够找到极大值。
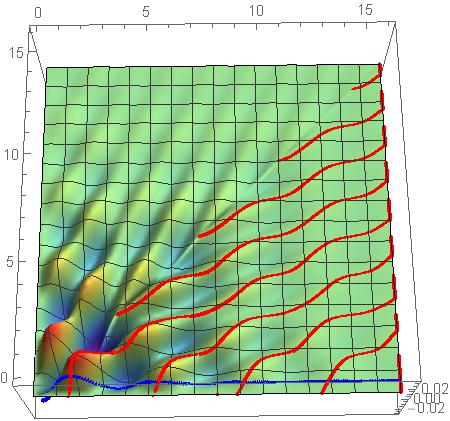
V1
对“脊”的定义不明确。所以随手写了一个。思路是t2固定时,寻找极大值位置的t1。
c1 = 3/5;
c2 = -3/10;
ck = 1/4;
k1 = 3;
k2 = 3/10;
H1[s_] := 1/(s^2 + c1*s + k1)
H2[s1_, s2_] := (2*k2 + ck (s1 + s2) + 2 c2*s1*s2)*H1[s1]*H1[s2]*H1[s1 + s2]/2
h2[t1_, t2_] = InverseLaplaceTransform[H2[s1, s2], {s1, s2}, {t1, t2}];
p1 = Plot3D[h2[t1, t2], {t1, 0, 16}, {t2, 0, 16}, PlotRange -> All,
Exclusions -> None, PlotPoints -> {80, 80},
ColorFunction -> "Rainbow", ImageSize -> 100];
expr = h2[t1, t2] /. HeavisideTheta[_, _] -> 0;(*只考虑t2<=t1的区间*)
cf = With[{expr = expr}, Compile[{{t1, _Real}, {t2, _Real}}, expr]];
data = Table[cf[t1, t2], {t2, 0, 16, 0.01}, {t1, 0, 16, 0.01}];
pos = Monitor[
Join @@ Table[{0.01 (First@# - 1), 0.01 (i - 1), Last@#} & /@
FindPeaks[data[[i]]], {i, Length@data}], i];
pos2 = Select[pos, #1 >= #2 & @@ # &];
Show[p1, Graphics3D[{Red, PointSize[0.01], Point[pos2]}],
Graphics3D[{Blue, Point[{#, 0.5, cf[#, 0.5]} & /@ Range[0, 16, 0.1]]}],
ImageSize -> 300]