mathematica绘制曲面交线

Question

最近要绘制两个曲面的交线，但是网上的方法都很繁琐，求助大家

求三维曲面z = (3 y Sin[x])/(2 + Cos[x])和y=1的交线

用下面这个方法比较.慢

ContourPlot3D[{z - (3 y Sin[x])/(2 + Cos[x]), y - 1}, {x, 0, 
  2 Pi}, {y, 0, 2 Pi}, {z, 0, 2}, Contours -> {0}, 
 ContourStyle -> Opacity[0], Mesh -> None, 
 BoundaryStyle -> {1 -> None, 
   2 -> None, {1, 2} -> {{Green, Tube[.03]}}}, Boxed -> False]

另外我想绘制含虚数的函数图像...

Plot[(3 I Sin[x])/(2 + Cos[x]), {x, 0, 2 Pi}]

一直没有找到好的办法...

Answer 1

2D交线：画的y=1时x-z的图像：

ListLinePlot[
 MeshCoordinates@
    DiscretizeRegion@
     RegionIntersection[
      ImplicitRegion[z == (3 y Sin[x])/(2 + Cos[x]), {x, y, z}], 
      ImplicitRegion[y == 1, {x, y, z}]] /. {a_, _, c_} :> {a, c} // 
  Sort]

问题2：

Plot[Evaluate[{Re[#], Im[#]} &[(3 I Sin[x])/(2 + Cos[x])]], {x, -2 Pi,
   2 Pi}]

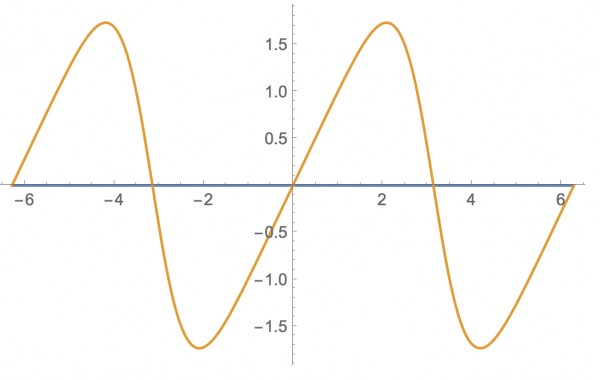
这个例子实数部分一直都是0

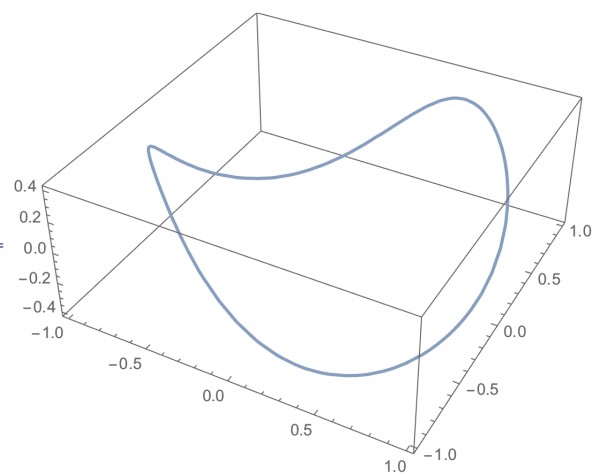
3D交线：

Show[DiscretizeRegion[
   RegionIntersection[
    ImplicitRegion[z == (3 y Sin[x])/(2 + Cos[x]), {x, y, z}], 
    ImplicitRegion[x^2 + y^2 + z^2 == 1, {x, y, z}]]], Boxed -> True, 
  Axes -> True, 
  Ticks -> Automatic] //. {Point -> 
   Nothing, {Line[a_]} :> {Thick, Line[a]}}

Comments

那我要是第二个曲面是x^2+y^2+z^2=1这个球面呢

---

稍等，我修改一下code加进答案

---

学习了 比我那个线条要细要自然 速度也快，谢谢

---

啊。。。刚给加粗，这样看起来像默认画出来的

---

已采纳 感觉跟着大家学到了很多 希望社区有更多人入驻

Answer 2

我只负责画图。最近一直在搞复变函数绘图。。

如果你要求x是实变量的话确实没什么乐子可看。

这证明了不是画图程序有错，而是本身整个函数图像就无聊.....没有实数部分。

复变的话乐子就大了。

3D或许直观些。

Comments

十分感谢...你经常在那个QQ群出没，我去那跟着你们学习

---

怪蜀黍我不约。。其实我也是新人一枚，去论坛的官方群365716997吧

Answer 3

用 MeshFunctions 是最好的解决方法。（下面代码 ContourPlot3D 里面也可以交换 f 与 g）

f = z - (3 y Sin[x])/(2 + Cos[x]);
g = x^2 + y^2 + z^2 - 1; 
ContourPlot3D[
 f == 0, {x, 0, 2 \[Pi]}, {y, 0, 2 \[Pi]}, {z, 0, 2}, 
 MeshStyle -> Red, ContourStyle -> Opacity[0.1], 
 MeshFunctions -> 
  Function[g /. {x -> Slot@1, y -> Slot@2, z -> Slot@3}], 
 Mesh -> {{0}, {0}, {0}}, BoundaryStyle -> None, Boxed -> False, 
 Axes -> False]

范围不限制在第一象限，如下图。