如何实现压平列表的最内层？

Question

例如：

{{a, b}, {c, {d}, e}, {f, {g, h}}}

希望实现的结果为：

{{a, b}, {c, d, e}, {f, g, h}}

再例如：

{{{a},{b},{c},d},{e}}

希望实现的结果为：

{{a,b,c,d},{e}}

我使劲倒弄Flatten，可是怎么弄都好像不对.....

===========================================================

利用TreeForm对最内层下一个定义。

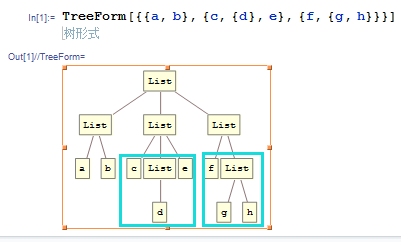
只有TreeForm产生的图的全体最终节点（最内层）中的元素被取出，并且放入到对应的上一节点内（压平）。又如：

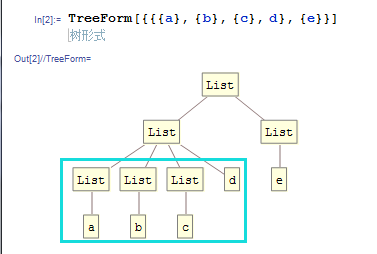
以及：

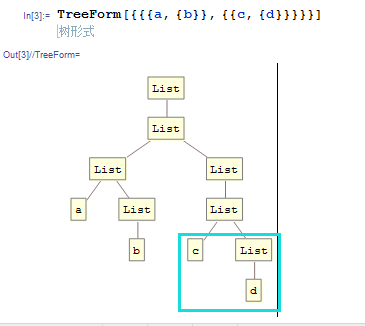
还有：

================================================

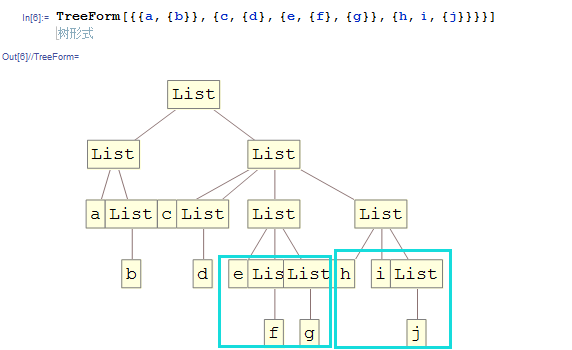
发现了一个比较严重的问题。好像各位都完全没考虑列表元素是符号值的情况啊。

出错示例：

In[94]:= flattenMostInner=Map[#/.{{x___}:>x,x___:>x}&,#,{Depth[#]-2}]&;
flattenMostInner2=Map[#/.{x_List:>Flatten@x}&,#,{Depth[#]-3}]&;
flattenMostInner3=Apply[Sequence,#,{Depth[#]-2}]&;
test0={{{a},{b}},{{c,{d}},{e},{f},{{g},{h}}}};
test1=List[List[List[Hue[0.5107930946784643`,0.8354307161342199`,0.7718521452428755`]],List[Hue[0.5113169196285673`,0.8358213579394708`,0.7713657815095133`]]],List[List[Hue[0.192618226271086`,0.8755716287620745`,0.7116923362420707`],List[Hue[0.5107930946784643`,0.8354307161342199`,0.7718521452428755`]]],List[Hue[0.3731282181502969`,0.789529229678425`,0.8195909513398986`]],List[Hue[0.4076579648111174`,0.7921461731652201`,0.8172922377294225`]],List[List[Hue[0.192618226271086`,0.8755716287620745`,0.7116923362420707`]],List[Hue[0.3731282181502969`,0.789529229678425`,0.8195909513398986`]]]]];
test2={{{f[a]},{f[b]}},{{g[a],{g[b]}},{f[a]},{g[e]},{{h[a]},{h[b]}}}};
test3=
flattenMostInner@test0
flattenMostInner2@test0
flattenMostInner3@test0
flattenMostInner@test1//FullForm
flattenMostInner2@test1//FullForm
flattenMostInner3@test1//FullForm
flattenMostInner@test2
flattenMostInner2@test2
flattenMostInner3@test2
Out[100]= {{{a},{b}},{{c,d},{e},{f},{g,h}}}
Out[101]= {{{a},{b}},{{c,d},{e},{f},{g,h}}}
Out[102]= {{{a},{b}},{{c,d},{e},{f},{g,h}}}
Out[103]//FullForm= List[List[List[Hue[0.5107930946784643`,0.8354307161342199`,0.7718521452428755`]],List[Hue[0.5113169196285673`,0.8358213579394708`,0.7713657815095133`]]],List[List[Hue[0.192618226271086`,0.8755716287620745`,0.7116923362420707`],List[Hue[0.5107930946784643`,0.8354307161342199`,0.7718521452428755`]]],List[Hue[0.3731282181502969`,0.789529229678425`,0.8195909513398986`]],List[Hue[0.4076579648111174`,0.7921461731652201`,0.8172922377294225`]],List[List[Hue[0.192618226271086`,0.8755716287620745`,0.7116923362420707`]],List[Hue[0.3731282181502969`,0.789529229678425`,0.8195909513398986`]]]]]
Out[104]//FullForm= List[List[List[Hue[0.5107930946784643`,0.8354307161342199`,0.7718521452428755`]],List[Hue[0.5113169196285673`,0.8358213579394708`,0.7713657815095133`]]],List[List[Hue[0.192618226271086`,0.8755716287620745`,0.7116923362420707`],List[Hue[0.5107930946784643`,0.8354307161342199`,0.7718521452428755`]]],List[Hue[0.3731282181502969`,0.789529229678425`,0.8195909513398986`]],List[Hue[0.4076579648111174`,0.7921461731652201`,0.8172922377294225`]],List[List[Hue[0.192618226271086`,0.8755716287620745`,0.7116923362420707`]],List[Hue[0.3731282181502969`,0.789529229678425`,0.8195909513398986`]]]]]
Out[105]//FullForm= List[List[List[Hue[0.5107930946784643`,0.8354307161342199`,0.7718521452428755`]],List[Hue[0.5113169196285673`,0.8358213579394708`,0.7713657815095133`]]],List[List[Hue[0.192618226271086`,0.8755716287620745`,0.7116923362420707`],List[0.5107930946784643`,0.8354307161342199`,0.7718521452428755`]],List[Hue[0.3731282181502969`,0.789529229678425`,0.8195909513398986`]],List[Hue[0.4076579648111174`,0.7921461731652201`,0.8172922377294225`]],List[List[0.192618226271086`,0.8755716287620745`,0.7116923362420707`],List[0.3731282181502969`,0.789529229678425`,0.8195909513398986`]]]]
Out[106]= {{{f[a]},{f[b]}},{{g[a],{g[b]}},{f[a]},{g[e]},{{h[a]},{h[b]}}}}
Out[107]= {{{f[a]},{f[b]}},{{g[a],{g[b]}},{f[a]},{g[e]},{{h[a]},{h[b]}}}}
Out[108]= {{{f[a]},{f[b]}},{{g[a],{b}},{f[a]},{g[e]},{{a},{b}}}}

==============================================================

此外，必须更加精密地定义最底层的概念。节点的长度，理应是根据FullFrom的头部为List的节点作计算的。

因此例如：

{a, {b, g[g[g[{c, {d}}]]]}}

应该得到：

{a, b, g[g[g[{c, {d}}]]]}

诸如以下的：

{a -> {1, {2, {3}}}, {b :> {2, {3}}, {c, {d}}}}

应该得到：

{a -> {1, {2, {3}}}, {b :> {2, {3}}, {c, d}}}

因为：

In[116]:= {a->{1,{2,{3}}},{b:>{2,{3}},{c,{d}}}}//FullForm
Out[116]//FullForm= List[Rule[a,List[1,List[2,List[3]]]],List[RuleDelayed[b,List[2,List[3]]],List[c,List[d]]]]

理应只有List[C,List[d]]被压平。

==========================================

为什么Atom的识别是无歧义非人为的：

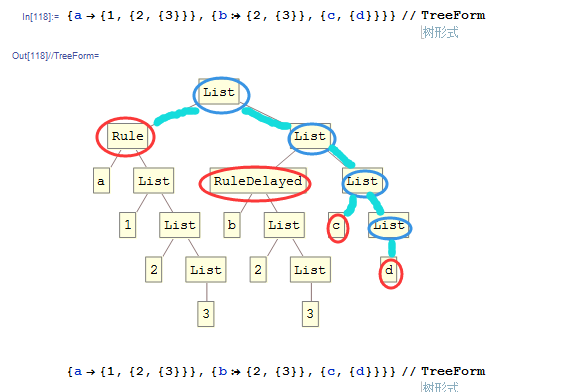
只有List作为头部的节点才能计算层数。在FullForm和TreeForm是掩盖不了的。又如：

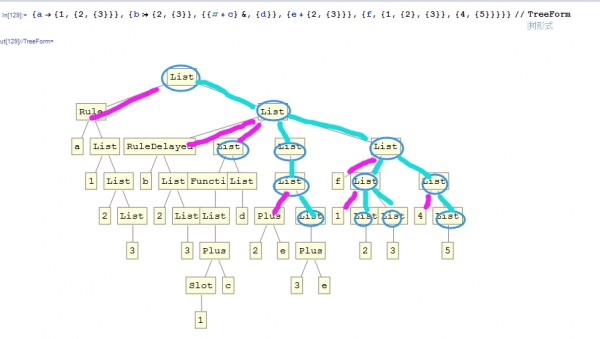
蓝色线是表示满足最底层的分叉，蓝圈是对于flattenMostInner有意义而不是视为一个单独Atom的节点。本质上来说这是一个图论问题。

Comments

除了Flatten函数，还有Map呀。

---

看到的定义Map就怂了- -就会最基础的用法

---

你倒是把测试数据给贴出来啊！！！！！手打一堆list就已经够过分了，还打算让我手打Hue。

---

论坛对Hue的支持有问题，转了FullFrom。刚才去吃饭了。。。、

---

我也给了一种能用的答案，可以参考一下

Answer 1

flatten = 
  ReplacePart[#, MaximalBy[Position[#, List], Length] -> Sequence] &;
flatten@test0
flatten@test1
flatten@test2

直接寻找层次最深的List头部，然后替换。所以请不要出现f[{1,2,3}]这种可能需要被人为当成一个Atom的表达式。
 

补充：正好你的例子出现了我上面说的情况。

{a -> {1, {2, {3}}}, {b :> {2, {3}}, {c, {d}}}}

这里{2, {3}}就被人为当成Atom不需要进行Flatten，而{c, {d}}却不是。那么问题又来了，判断是否是Atom的标准是？

补充2：

test0 = {{{a}, {b}}, {{c, {d}}, {e}, {f}, {{g}, {h}}}};
test1 = {{{Hue[0.51, 0.83, 0.77]}, {Hue[0.51, 0.83, 0.77]}}, 
     {{Hue[
     0.19, 0.87, 0.71], {Hue[0.51, 0.83, 0.77]}}, {Hue[0.37, 0.78, 0.81]},
     {Hue[0.40, 0.79, 0.81]}, {{Hue[0.19, 0.87, 0.71]}, 
     {Hue[0.37, 0.78, 0.81]}}}};
test2 = {{{f[a]}, {f[b]}}, {{g[a], {g[b]}}, {f[a]}, {g[
      e]}, {{h[a]}, {h[b]}}}};
test3 = {a -> {1, {2, {3}}}, {b :> {2, {3}}, {c, {d}}}};

FindHeadPath[expr_, end_] := 
  Table[Head[expr[[Sequence @@ end[[1 ;; n]]]]], {n, 
    Length@end - 1}];
getPos[expr_] := 
  Select[Position[expr, List], 
   SameQ @@ Flatten[{FindHeadPath[expr, #], List}] &];
flatten = ReplacePart[#, MaximalBy[getPos[#], Length] -> Sequence] &;
flatten@test0
flatten@test1
flatten@test2
flatten@test3

寻找所有List头部位置，然后搜索该路径涉及到的头部是否全部为List，然后flatten。

Comments

当然是指单参数的情况。FlattenMostInner单参数都未解决也不应该搞大跃进到多参数的情况。

---

再通俗地说，类似f[{1,{2,3}}]，它的FullFrom是f[List[1,List[2,3]]]，里面的List已经被前面的头f给“遮蔽”了，不能，不应纳入List头部长度的计算

---

已补充答案。已补充答案。

---

非常感谢。这次这个问题应该是完美地解决了。（不继续延伸下去到话。。。23333，不过再搞也是在层的定义或者层数，比如倒数第二层什么鬼的上面做手脚，不过那些暂时是用不上了，233）

---

这个技术含量真高，学习一个

Answer 2

我也补一种:

flattenMostInnerList[lst_List] := 
 ReplacePart[
  lst, (MaximalBy[
      Position[
       Replace[lst, 
         head_[expr__] :> {head, expr}, {0, 
          Infinity}] /. {Except@List, ___} -> foo, List, 
       Heads -> False], Length] - 1) -> Sequence]

注：下面回答只适用原问题：用于list, 最内层认为是expr tree的最内层。第三种要求最内层元素atomic。

flattenMostInner = 
 Map[# /. {{x___} :> x, x___ :> x} &, #, {Depth[#] - 2}] &

(忽略那个f的颜色)

又想出一种差不多的：

flattenMostInner2 = 
 Map[# /. {x_List :> Flatten@x} &, #, {Depth[#] - 3}] &

效果相同

又想到一种：

flattenMostInner3 = Apply[Sequence, #, {Depth[#] - 2}] &

 

Comments

额，为啥不Flatten/@list。。。

---

flatten最内层的话，比如说flattenMostInner@{{{a, {b}}, {{c, {d}}}}}这样的我觉得按照他的需求答案应该是{{{a, {b}}, {{c, d}}}}，直接map Flatten正好是对题中那两个例子有效，但是只是把level2以后的全Flatten了

---

那也是Map[f, list, {-Depth@list + 2}]呀。其实核心还是在于什么是最内层。问题描述的太含糊，自然以例子为准。

---

我感觉用负的level还是不行的，就比如说题主第一个例子，用负的level会把{a, b}也压平，但是按照他的要求不应该压平那个

---

嗯，确实在于最内层是怎么个意思

---

最后一种手动点赞。。。。

---

最内层当然可以下一个最精密的定义，按照TreeForm得到的树，里面最底层的项被提取，加入到最底层上一层的list中，这才是压平最内层。问题已更新。

---

问题修改后，同意最后一种Apply+Sequence的做法。前几种方法太累赘了。

---

还有没有什么其他的方法吗？我只能想到比较常见的

---

我发现一个比较严重的问题，flattenMostInner3会将列表元素中的Hue头给压没掉。一个列表不是全部的元素都是数值来的，有可能是符号值！

---

为了保全列表中可能出现的符号值，恐怕还是map+Flatten的结构比较妥当，就是map我实在不会....

---

所以请再给出更合理的例子。。

---

关于符号值的问题示例已更新。事实上，要完全解决这种问题我可能还漏了一种，列表元素里面里面含有#，或者其他模式匹配符号的情况。

---

你这是相当于改了需求，首先Depth本身不会考虑你的expression的head，这三种方法全都不能使用了。这种情况还是重新提问比较合适吧

---

@happyfish 是不断把模糊问题清晰化。所有这才是我一开始说以例子为准的原因，因为有时候语言描述太含糊。

---

对啊，按照例子来说我觉得就是两个问题了

---

其实这是一个编程习惯问题- -，我是习惯将每一个元素视为未知表达式的。为什么你们会将a,b,c,d,e....这些习惯想象成孤立的Atom或者数值呢= =。下次会注意的，麻烦了各位不好意思

---

@EmberEdison 因为考虑潜在的所有可能比较累。a看上去是“一个”字母。就像1是一个数字，但是我也可能在后续程序把1替换成复杂表达式。在没有贴出后续程序的时候，绝大部分人我想不会考虑到1是个复杂表达式的可能性。

---

我是用Clisp来编程的，所以已经完全习惯将symbol视为复杂表达式了....我一开始想表示的解决方法其实和最后的差不多，因为用二叉树来分析的话即使是对于复杂表达式也应该是普适的。

---

我就是可简单的理解来了。

---

忽然想起这个问题。我觉得mma不能把一个symbol当成任意表达式来看，否则任何问题都无法解决。比如Flatten[a]，你要是把a考虑为一个nested list，mma给出的答案还不对呢。或者说，a:=Quit[]